消费者选择的经济模型指的是人们总是选择他们能够负担的最优消费束，也即消费者从他们的预算集中选择最偏好的消费束。

1. 最优选择

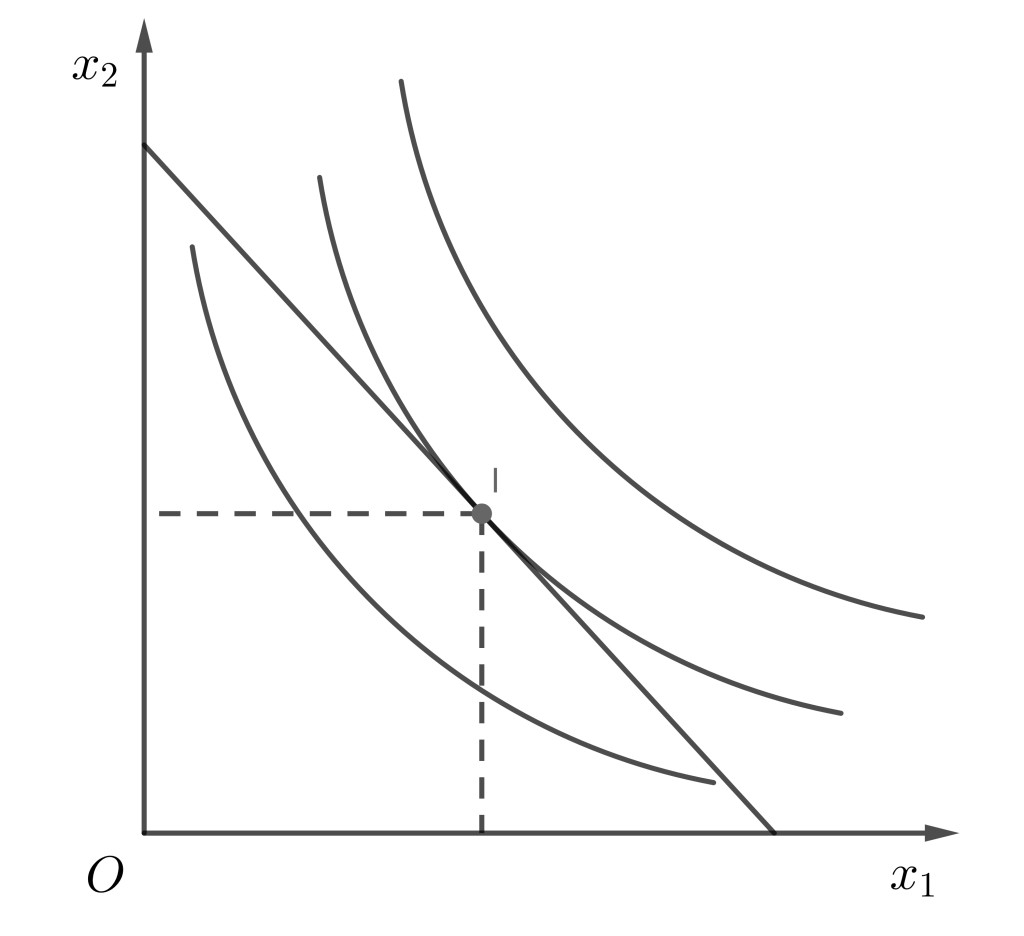
在一般情况下，最优选择的必要条件为预算线与无差异曲线斜率相同，也即二者相切。因为若不相切，预算线将会穿过无差异曲线，从而会存在更优消费束。

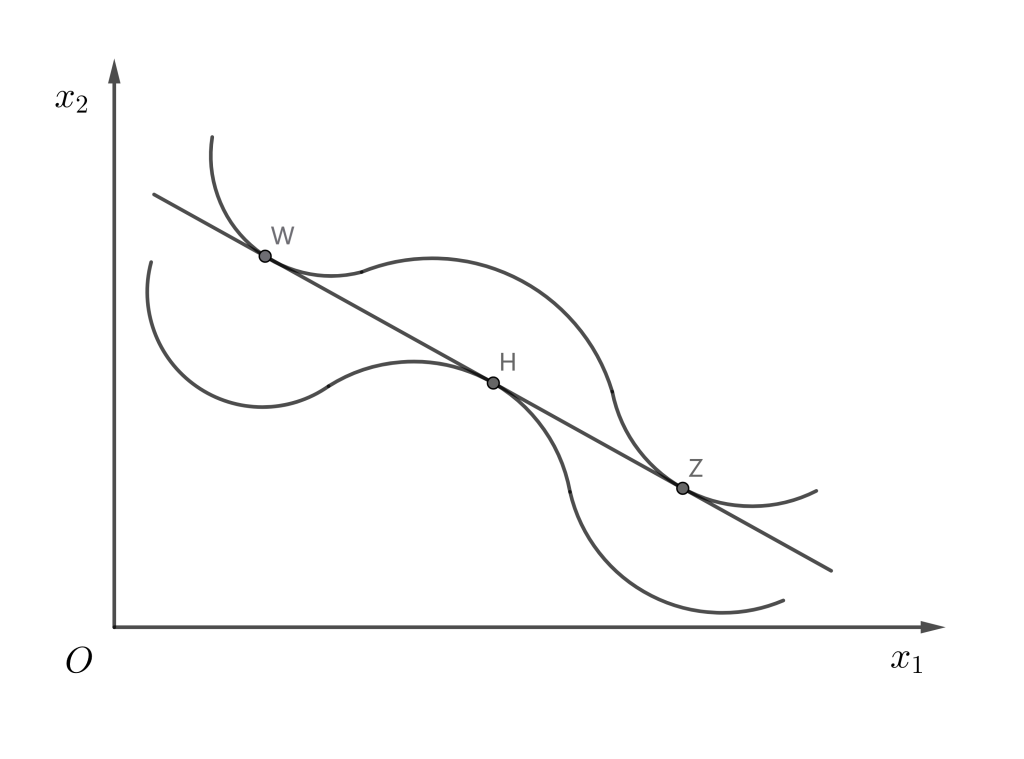
但相切并非充分条件，除非是凸偏好的无差异曲线。

在最优选择处，$MRS = -\frac{p_1}{p_2}$。前者表示消费者愿意进行商品交换的比例，而后者则为实际市场进行商品交换的比例。

2. 消费者需求

一定价格水平下的商品1和商品2的最优选择，称作消费者的需求束。需求函数是最优选择的商品数量与价格、收入的函数。以$x_1$为例，记为$x_1(p_1,p_2,m)$，这是我们的研究重点。

3. 需求函数的具体例子

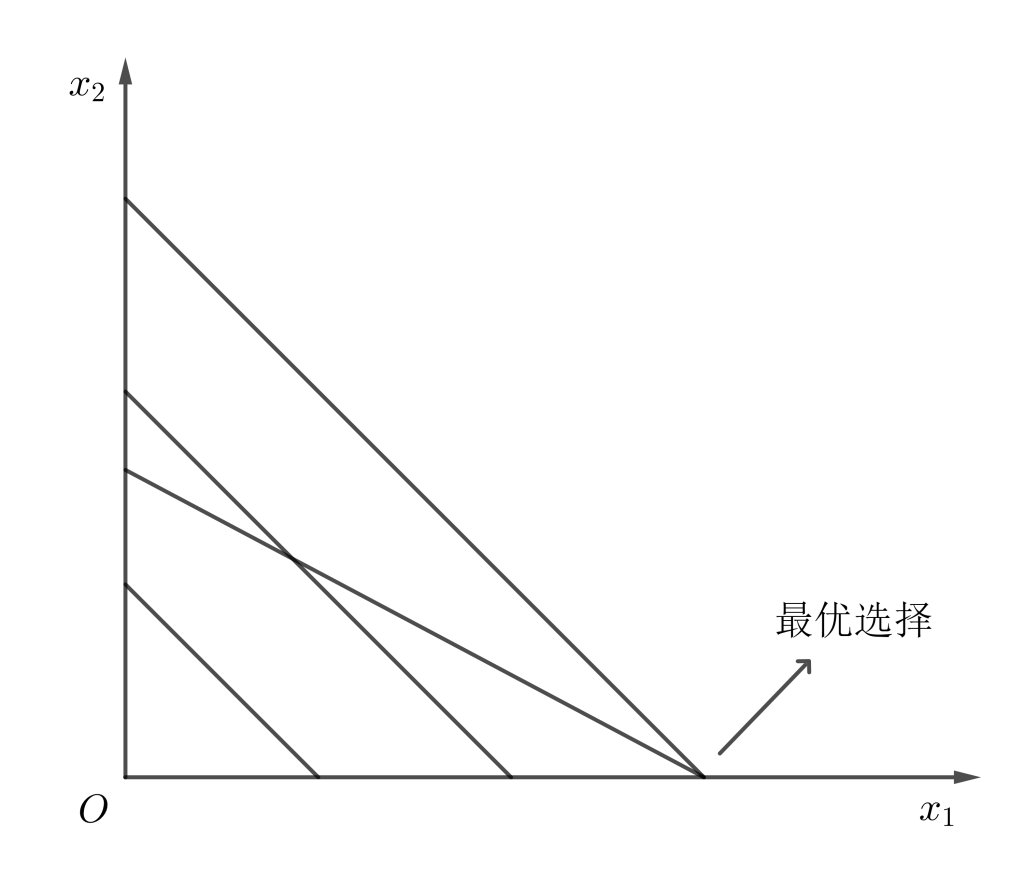
3.1 完全替代

这里以替代率为1:1为例， $$ x_1= \begin{cases} m/p_1 &p_1<p_2 \\ [0,m/p_1] &p_1=p_2 \\ 0 &p_1 >p_2 \end{cases} $$

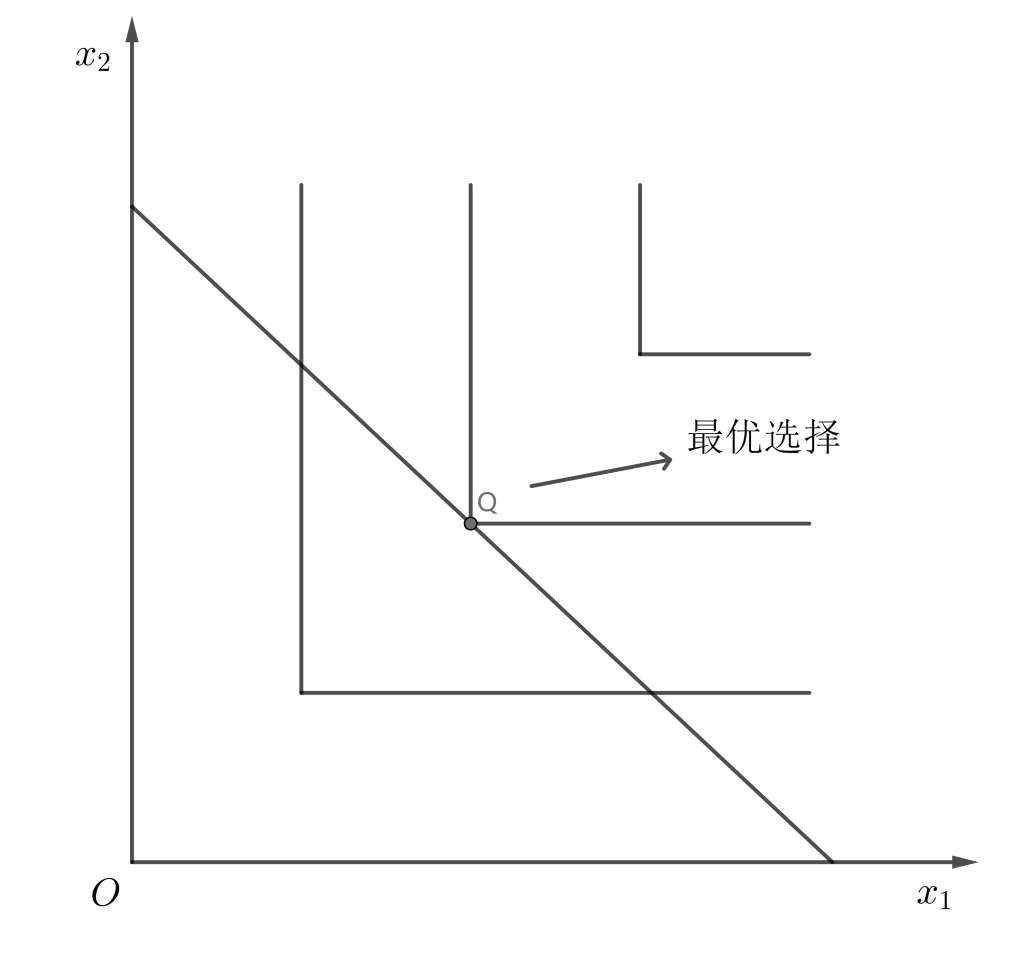
3.2 完全互补

这里以互补率为1:1为例，对于预算约束线$p_1x_1 + p_2x_2 = m$，令$x_1 = x_2$，进一步求解有： $$ x_1 = m/(p_1 +p_2) $$

3.3 中性商品和厌恶品

对于这两类商品（$x_2$），由于消费者会将所有钱花在更偏好的商品上（$x_1$），因此有： $$ \begin{align*} x_1 &= \frac{m}{p_1} \\ x_2 &= 0 \end{align*} $$

3.4 柯布-道格拉斯偏好

假定效用函数采用以下形式： $$ u(x_1,x_2) = x_1^c x_2^d $$

对于最优选择有： $$ \begin{align*} x_1 &= \frac{c}{c+d} \frac{m}{p_1} \\ x_2 &= \frac{d}{c+d} \frac{m}{p_2} \end{align*} $$

柯布-道格拉斯偏好可以通过指数项判断消费者在不同商品上的花费占收入的比例。具体地，若消费者在商品1上的花费为$p_1 x_1$，那么该比例为： $$ \frac{p_1x_1}{m} = \frac{p_1}{m} \frac{c}{c+d} \frac{m}{p_1} = \frac{c}{c+d} $$

因此，如果写为$u(x_1,x_2) = x_1^a x_2^{1-a}$的形式将会非常方便地表示消费比例。

4. 求解效用最大化的方法

对于在一个条件约束下求解效用最大化的问题（如下），一般有两种方法。 $$ \begin{align*} \max_{x_1,x_2} \quad&u(x_1,x_2)\ \\ \text{s.t.} \quad &p_1x_1 + p_2x_2 = m \end{align*} $$

4.1 一阶微分法

由约束条件得到： $$ x_2(x_1) = \frac{m}{p_2} - \frac{p_1}{p_2}x_1 $$

代入效用函数中转换为对$x_1$求最大化： $$ \max \quad u(x_1,\frac{m}{p_2} - \frac{p_1}{p_2}x_1) $$

根据函数最大化的必要条件对$x_1$求一阶微分并令其等于0有： $$ \frac{\partial u(x_1, x_2(x_1))}{\partial x_1} + \frac{\partial u(x_1,x_2(x_1))}{\partial x_2} \frac{\text{d}x_2}{\text{d}x_1} = 0 $$

对$x_2(x_1)$求微分有： $$ \frac{\text{d}x_2}{\text{d}x_1} = - \frac{p_1}{p_2} $$

代入一阶微分条件式中有： $$ \frac{\partial u(x_1^*, x_2^*) / \partial x_1}{\partial u(x_1^*, x_2^*) / \partial x_2} = \frac{p_1}{p_2} $$

此式恰恰为$MRS = - \frac{p_1}{p_2}$，也即最优选择需满足的条件。再结合预算约束线方程，一共两个方程两个未知数，即可求解。

4.2 拉格朗日乘数法

首先构造辅助函数： $$ \mathscr{L} = u(x_1,x_2) - \lambda(p_1x_1 +p_2x_2 - m) $$

其中，$\lambda$为拉格朗日乘数。根据拉格朗日定理，最优选择$(x_1^*,x_2^*)$必满足三个一阶微分条件： $$ \begin{align*} \frac{\partial \mathscr{L}}{\partial x_1} &= \frac{\partial u(x_1^*, x_2^*)}{\partial x_1} - \lambda p_1 &= 0 \\ \frac{\partial \mathscr{L}}{\partial x_2} &= \frac{\partial u(x_1^*, x_2^*)}{\partial x_2} - \lambda p_2 &=0 \\ \frac{\partial \mathscr{L}}{\partial \lambda} &= p_1x_1^* + p_2x_2^* -m &= 0 \end{align*} $$

三个方程，三个未知数，可以进一步进行求解。

另外，由1式除以2式可以得到之前的关系式： $$ \frac{\partial u(x_1^*, x_2^*) / \partial x_1}{\partial u(x_1^*, x_2^*) / \partial x_2} = \frac{p_1}{p_2} $$

而3式就是我们的预算约束条件。因此该方法本质上与方法1一致。